Model Validation for Supervised Models

Model Validation is based on the statement that after selecting the appropriate model and its hyperparameters, we can determine how the model is performing and how much accuracy is the model gives while testing for some known accuracy. There are mainly two ways for validating a model as follow:

In this methodology, we at first hold back some subset of the data from the training dataset, and then apply this holdout set to check the model's performance. We can do this by splitting the training dataset. For this purpose, we can make use of the train_test_split utility available in Scikit-Learn.

let's demonstrate this using a dataset from sklearn library. We will first start by loading the data:

Now, we choose a model and hyperparameters. For this application, we are going to make use of the k-neighbors classifier with n_neighbors=1. k-neighbors classifier is a very is a simple model that says "the label of unknown point in a set is same as the label of its closest neighboring training point":

Now that we have our data and model ready let1s split the data and run our model:

The output of above code is:

which is a reasonable accuracy of the model. It depicts that the nearest-neighbor classifier is about 90% accurate on this holdout set.

One disadvantage of using the previous approach for model validation is that we have lost some part of our data to the model training. In the previous case, half the dataset does not contribute to the training of the model. This is not optional and can cause problems, especially if the initial set of training data is small.

One way to address this issue is to use cross-validation i.e. to do a sequence of fits where each subset is used both as a training set and as a validation set. Graphically cross-validation can be represented as below:

Here we run validation twice, alternately using each half of the data as a holdout set. By using the split data above we can implement our model like this:

what comes out are two accuracy scores, which we could combine; for instance by calculating mean, to get a better measure of the global performance. This form of cross-validation is called two-fold cross-validation, one in which we have to split the data into two sets and used both in turn as a validation set.

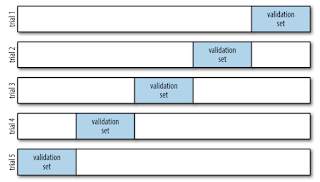
We could dive deeper into this idea to use even more splits and more folds in the data. A five-fold cross-validation is depicted in the graph below:

In five-fold cross-validation, we split the data into five different groups, and use each of the groups in turn to evaluate the model fit on the other remaining groups. This can be a very tedious task to do by hand, and so to make it easy there is  a Scikit-Learn's cross_val_score convenience routine to to perform it simply:

Repeating the validation across different subsets of the data gives us an even better idea of the performance of the algorithm.

Scikit-Learn includes a number of cross-validation approaches that are useful in particular scenarios: these are implemented using iterators in the model_selection module. For instance, we might want to go to the extreme case in which a total number of split data groups is equal to the number of data points; that is, we train our model on all points. This type of cross-validation scheme is referred to as leave-one-out cross-validation, and it can be implemented as follows:

Since there were 150 samples, the leave-one-out cross-validation concludes scores for 150 trials, and the score depicts either successful (1.0) or unsuccessful (0.0) predictions. By taking the average of these outputs, it gives an estimation  of the error rate:

Other cross-validation schemes can be used similarly. For a description of what is available in Scikit-Learn, use Ipython to explore the sklearn-model_selection sub-module or take a look at Scikit-Learn's online cross-validation documentation.

Now that we’ve seen some of the basics of model validation, we will go a little deeper regarding the selection of models and the selection of hyperparameters. These issues are some of the most important aspects of practicing machine learning, and I find that this information is often skipped over in introductory machine learning courses. Of core importance are the questions: if our model is performing bad, how should we move on to the next level? There are several possible answers: 

The answer to this question is often misunderstood or misinterpreted. To be specific, sometimes while using a more complicated/flexible estimator will give worse results, and adding more training samples may not improve our results! The ability to predict or conclude what steps will improve the performance of our model is what separates the successful machine learning practitioners from the unsuccessful.

We will write more about selecting the best model in another article please stay tuned.

The Google Colab link to this article can be found here.